Oberstufe
W.13 | Baumdiagramm, Vierfeldertafel
Die einfachste Möglichkeit, einen Sachverhalt in der Wahrscheinlichkeitsrechnung zu veranschaulichen, ist ein Baumdiagramm oder eine Vierfeldertafel.
Es gibt zwei gute Möglichkeiten, Wahrscheinlichkeiten zu veranschaulichen: das Baumdiagramm und die Vierfeldertafel.
Ein Baumdiagramm kann man theoretisch immer malen, das ist auch klasse und ganz toll. Leider hat es den Nachteil, dass es sehr schnell kompliziert wird.
Die Vierfeldertafel kann man anwenden, wenn man es mit genau zwei Ausprägungsmerkmalen [=betrachtete Eigenschaften] zu tun hat.
W.13.01 | Baumdiagramm (mit; ohne Zurücklegen)
Ein Baum ist eigentlich nichts anderes als ein Schema, in welchem alle möglichen Ausgänge und Geschehnisse verzeichnet sind.
|
1. Die Summe aller Wahrscheinlichkeiten, die von einer Verzweigung ausgehen, ist 1. 2. Innerhalb eines Pfades werden Wahrscheinlichkeiten multipli-ziert. 3. Die Wahrscheinlichkeiten. von verschiedenen Pfaden werden addiert. |

Beispiel a.
Anni K. hat einen Apfel, eine Birne und eine Cirsche vor sich liegen, von denen sie nur eine essen möchte. Sie kann die Frucht im Schaukelstuhl oder in der Hängematte essen. Erfahrungsgemäß entscheidet sie sich in 70% der Fälle aus Bequemlichkeit für den Schaukelstuhl und greift dann zufällig zu einer Frucht.
a) Veranschaulichen Sie den Sachverhalt in einem Baumdiagramm!
b) Mit welcher Wahrscheinlichkeit isst Anni einen Apfel?
Lösung:
a) Hier ein Beispiel, wie man das Baumdiagramm falsch beginnen könnte:
In einem Baum gehen von einem Verzweigungspunkt immer alle denkbaren Entscheidungsmöglichkeiten aus, von denen immer genau eine eintreffen wird!
Zuerst entscheidet sich Anni zwischen den beiden Möglichkeiten „Schaukelstuhl“ und „Hängematte“. Daher führt die erste Verzweigung im Baum auf diese beiden Auswahlmöglichkeiten.
Danach erst entscheidet sich Anni K. für eine der Früchte. Und zwar entscheidet sie sich für die Früchte, egal ob sie in der Hängematte rumhängt oder im Schaukelstuhl schaukelt. Daher gibt es sowohl nach „Schaukelstuhl“ als auch nach „Hängematte“ die neue Verzweigung zwischen „Apfel“, „Birne“ und „Cirsche“.
Da Anni zufällig nach den Früchten greift, hat jede Frucht die Wahrscheinlichkeit von 1/3.

b) Anni soll also nen Apfel essen. Das ist gut, das ist nämlich gesund.
Allerdings interessiert uns eher die Wahrscheinlichkeit davon. Sie sollten jetzt auf die Idee kommen, dass es zwei Möglichkeiten gibt, den Apfel zu essen:
Anni kann im Schaukelstuhl den Apfel essen oder sie kann ihn in der Hängematte essen. Im Baumdiagramm sind das die beiden Pfade: „Schaukelstuhl-Apfel“ und „Hängematte-Apfel“ (abgekürzt: S-A und H-A).
Der Pfad „S-A“ hat die W.S. von 0,7·1/3 der Pfad „H-A“ hat die W.S.: 0,3·1/3.
Wenn man die W.S. beider Pfade addiert, erhält man dann die gesamte W.S., dass die hübsche Anni den noch hübscheren Apfel isst.
Mathematisch könnte man das Ganze so formulieren: P(Apfel) = P(S-A, H-A) = 0,7·1/3+0,3·1/3 ≈ 0,333
Die ersten Teilaufgaben von Prüfungen und Klausuren sind meist nicht so komplex, so dass man ganz gut ein Baumdiagramm erstellen kann. Leider werden die Aufgaben oft zu komplex für einen Baum [Sie möchten mit Sicherheit keinen Baum erstellen, der beispielsweise 1200 Verzweigungen hat].
Manchmal gibt es zwar nicht viele Verzweigung in einem Baum, jedoch ist die Aufgabenstellung so verwirrend, dass ein Baum sinnvoll ist [siehe Beispiel d. und Beispiel e.].
Beispiel b.
An einem Apfelbaum hängen 12 rote, 8 gelbe und 5 braune Äpfel. Barbara rüttelt gierig am Baum und tatsächlich fallen zwei Früchte herunte
a) Erstellen Sie ein Baumdiagramm.
b) Mit welcher W.S. haben beide Früchte die gleiche Farbe?
c) Mit welcher W.S. ist der erste Apfel gelb?
d) Mit welcher W.S. ist genau ein Apfel braun?
e) Mit welcher W.S. ist mindestens ein Apfel rot?
Lösung:
Es handelt sich natürlich um Ziehen ohne Zurücklegen [wenn ein Apfel einmal runter fällt, kann er ja nicht noch einmal runter fallen].

d) In dieser Teilaufgabe interessieren wir uns nicht alle Farben, sondern nur die Farben „braun“ oder „nichtbraun“. Wir fassen daher rote und gelbe Äpfel einfach zu nichtbraunen zusammen. Am Baum hängen also 5 braune und 20 nichtbraune Äpfel. Wenn genau ein Apfel braun sein soll, kann das entweder der erste oder der zweite Apfel sein. Es gibt daher die Möglichkeiten



Beispiel c.
Maria und Benni machen 5 Tage (und Nächte) lang Urlaub auf einem Bauernhof in einem kleinen Örtchen bei Schramberg. Hier regnet es im Durchschnitt an 5 Nächten pro Woche. Das ist schlecht, denn die beiden träumen von einer wilden Liebesnacht unter freiem Himmel.
Wie hoch ist die Chance, dass die beiden ihren Traum erfüllen können ?
Lösung:

Natürlich gibt es auch hier eine einfachere Methode. (Über´s Gegenereignis)
Wir überlegen uns dazu, was passieren müsste, damit es zu keiner Liebesnacht kommen kann. Wenn man sich den Baum anschaut, sieht man, dass es dazu in jeder Nacht regnen müsste.

Beispiel d.
Maria versucht ihrem Freund Benni die frohe Botschaft mitzuteilen, dass die schwanger ist. Leider hat er das Handy ausgeschaltet und ist im Jugendtreff, was sie jedoch nicht weiß. Für sie kommen vier Möglichkeiten in Frage, wo er sein kann: Zuhause, im Pub, an der Hochschule oder im Jugendtreff. Nun fährt sie alle Stationen zufällig ab.
a) Fertigen Sie ein Baumdiagramm.
b) Mit welcher Wahrscheinlichkeit trifft Maria Benny beim zweiten Versuch?
c) Mit welcher Wahrscheinlichkeit braucht Maria mindestens zwei Versuche?
Lösung:
.jpg)
Nun ja, das war wirklich eine sehr schöne Aufgabe und ein sehr, sehr schöner Baum, aber aus Sicht eines Mathematikers [und sicherlich auch aus Sicht eines Schülers] doch etwas viel Arbeit.
Das Ganze geht doch etwas einfacher, wenn man sich Folgendes überlegt: In der ganzen Aufgabe interessiert uns ja nur, ob Maria zum Jugendtreff geht oder zu den anderen drei Stationen.
Wir malen also nicht stupide den ganzen Baum auf, sondern nur so weit er für die Aufgabe interessant ist. Wir fassen daher die Stationen „Pub“, „Zuhause“ und „Hochschule“ zu einem einzigen Fall zusammen, zum Fall „Nicht-Jugendtreff“ 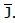 . Also machen wir die ganze Aufgabe, also den ganzen Baum, nochmal von vorne mit deutlich weniger Ästen.
. Also machen wir die ganze Aufgabe, also den ganzen Baum, nochmal von vorne mit deutlich weniger Ästen.

Beispiel e.
Drei Einzeller schwimmen zusammen in einem Teich herum. Alle 10 Sekunden stoßen sie auf einen Festkörper, bei welchem es sich entweder um einen Giftstoff oder um einen Nährstoff handelt. Wenn es sich um einen Giftstoff handelt, stirbt einer der Einzeller sofort. Handelt es sich um einen Nährstoff, startet einer der Einzeller umgehend eine Zellteilung [so dass danach ein Einzeller mehr vorhanden ist]. Unter der Annahme, dass es sich bei den relevanten Festkörper bei 60% um Nährstoffe handelt, wie hoch ist die Wahrscheinlichkeit dass nach:
a) nach 30 Sekunden kein Einzeller mehr vorhanden ist ?
b) sich nach 30 Sekunden die Anzahl der Einzeller verdoppelt hat ?
c) nach 30 Sekunden die Anzahl der Einzeller unverändert ist ?
d) nach 20 Sekunden die Anzahl der Einzeller unverändert ist ?
e) nach einer Minute noch mindestens ein Einzeller lebendig herumschwimmt ?
Lösung:
Vermutlich haben Sie die Aufgabe nicht sofort auf Anhieb durchschaut. Es wäre daher überlegenswert, ob man einen Baum zeichnet [Überlegenswert! Nicht ratsam! Man könnte die Aufgabe auch durchaus ohne Baumdiagramm lösen.].
Der interessante Punkt ist immer wieder das Ereignis „N“ [Nährboden] oder „G“ [Giftstoff], welche mit einer W.S. von P(N)=0,6 bzw. P(G)=0,4 eintreffen.
Um den Überblick [auch mit der Anzahl der Einzeller] nicht zu verlieren, sollten Sie sich überlegen, wie Sie den Baum im Detail aufbauen.
Im Folgenden habe ich den Baum so aufgebaut, dass ich nach den Buchstaben „N“ oder „G“ in Klammer notiert habe, wieviel Einzeller nach dem Treffen mit dem Festkörper vorhanden sind.
e) Eine Minute sind sechs Durchgänge. Wenn Sie einen Baum für sechs Durchgänge zeichnen wollen, haben Sie am Ende 32 Verzweigungen. Ich glaube, diesen Baum möchten Sie nicht zeichnen.
Wir versuchen die Aufgabe also ohne Baum zu lösen.
Dass nach sechs Durchgängen mindestens ein Einzeller da ist... das ist recht kompliziert. Das Gegenereignis wäre, dass kein Einzeller mehr lebt. Dieser [äußerst traurige] Fall ist etwas einfacher.
Wir überlegen also, welche Möglichkeiten existieren, dass nach sechs Durchgängen kein Einzeller mehr existiert.
Dreimal Giftstoffe: GGG
Viermal Giftstoffe [einmal Nährboden]: NGGGG, GNGGG, GGNGG, GGGNG (Beachten Sie: GGGGN gibt es nicht, da ja nach GGG bereits Schluss wäre.)
Fünfmal Giftstoffe [einmal Nährboden] geht nicht, es käme nie zum letzten „G“
= 0,43+0,6·0,44+0,4·0,6·0,43+0,42·0,6·0,42+0,43·0,6·0,4 ≈ 0,125
⇒ P(mindestens ein Einzeller ) = 1–0,125 = 0,875 ? 87,5%
Die Vierfelder-Tafel verwendet man, wenn es genau zwei Ausprägungsmerkmale gibt [z.B. männlich/weiblich und Rentner/Nichtrentner]. Meistens kann man statt der Vierfelder-Tafel auch einen Baum zeichnen, es gibt aber wenige Ausnahmen in welcher ein Baumdiagramm sehr ungeschickt wäre. [siehe weiter unten, Beispiel g.]
Beispiel f.
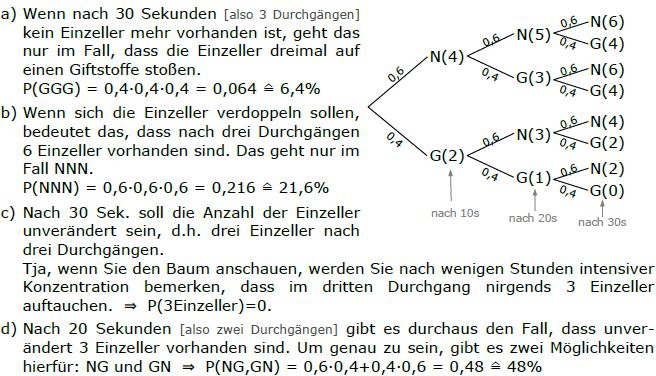
In einer Arztpraxis sind 70% der Patienten Rentner, 60% sind weiblich.
Wieviel berufstätige Männer sind bei 200 Patienten zu erwarten, wenn 50% weibliche Rentner sind?
Lösung
Man erstellt immer eine Tabelle mit vier Zeilen und vier Spalten. In der ersten Zeile und ersten Spalte stehen nur die Bezeichnungen, in der letzten Zeile und letzten
Spalte stehen die gesamten Häufigkeiten.
In unserem Beispiel steht die zweite Spalte für „männlich“, die dritte Spalte für „weiblich“, die zweite Zeile für „Rentner“ und die dritte Zeile für „Nichtrentner“. Da es insgesamt 70% Rentner hat, steht am Ende der Rentner-Zeile „0,7“. Da es 60% Frauenanteil hat, steht am Ende der Weiblich-Spalte „0,6“. [Rechts unten steht in jeder Vierfelder-Tafel eine „1“, da insgesamt immer 100% vorhanden sind]. Es gibt 50% weibliche Renter, also steht im Eintrag, der sowohl in der Rentnerzeile, als auch in der Weiblich-Spalte steht, eine „0,5“.

Die Zahlen im Rest der Felder leitet man sich nun durch einfache Subtraktion her [zweite Tafel!].
Als letzten Eintrag erhält man die [fett geschriebene] 0,2 und zwar entweder durch Rechnung in der Männlich- Spalte oder aus der Nichtrenter-Zeile. Damit haben wir auch schon die Antwort: Es gibt 20% männliche Berufstätige, was bei 200 Patienten: 0,2·200 = 40 Personen entspricht.
Beispiel g.
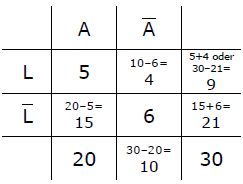
In einem Viertel aller Tage, an denen Katrin mit dem Auto zur Arbeit fährt, nimmt sie den Laptop mit. Im letzten Juni war das 5 Mal. An sechs Tagen fuhr sie jedoch weder mit dem Auto, noch nahm sie den Laptop mit. In wieviel Prozent aller Tage, an denen sie keinen Laptop mit nahm, fuhr sie mit dem Auto?
Lösung
Der Juni hat 30 Tage, das ist die Gesamtanzahl aller betrachteten Tage. Diese Zahl „30“ steht also rechts unten in der Tabelle. [Selbstverständlich könnte man statt mit der Absolutanzahl der Tage, auch mit deren prozentualer Häufigkeit rechnen (so wie in der letzten Aufgabe). Das ist völlig egal].
Die beiden betrachteten Merkmale sind Laptop bzw kein Laptop, also L bzw. L und Auto bzw kein Auto, also A bzw. A.
An fünf Tagen fuhr Katrin mit dem Auto und nahm den Laptop mit, daher steht die Zahl 5 in der „A“-Spalte und in der „L“-Zeile gleichzeitig. Diese eben genannten 5 Tage sind ein Viertel aller Tage, in welchen sie mit dem Auto hin fährt, also fährt sie an 20 Tagen mit dem Auto.
An 6 Tagen fuhr sie weder mit dem Auto, noch nahm sie den Laptop mit. Die Zahl „6“ steht demnach wieder an der entsprechenden Stelle.
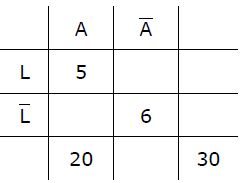
Den Rest der Zahlen errechnen wir primitiv.
→ Nun zur ursprünglichen Frage: „In wieviel Prozent aller Tage, an denen sie ohne Laptop fuhr, nahm sie das Auto?“.

Ohne Laptop ist sie an 21 Tagen gefahren [LZeile], davon an 15 Tagen mit dem Auto. Das entspricht 15/21 ≈ 0,714 ? 71,4%.
Beispiel h.
Katze „Mathilde“ und Kater „Cosinus“ fangen beide gelegentlich Feld- und Spitzmäuse [und das, obwohl beide Katzen eigentlich ausreichend fettgefressen sind]. Mathilde fängt 65% aller Mäuse, welche insgesamt zu 75% aus Spitzmäusen bestehen. 40% aller Feldmäuse werden von Cosinus gefangen.
Wieviel Prozent der Spitzmäuse werden von Mathilde gefangen?
Lösung:
Notieren wir mal alles, was uns gegeben ist:
? 65% aller Mäuse werden von Mathilde gefangen. In der M-Zeile steht hinten 0,65.
? Damit werden 35% aller Mäuse von Cosinus gefangen ⇒ in der C-Zeile steht hinten 0,35.
? Die Spitzmäuse machen 75% ALLER Mäuse aus ⇒ in der S-Spalte steht unten 0,75
? Die Feldmäuse machen also logischerweise 25% aller Mäuse aus.
? Der größte Trick an der Aufgabe: 40% aller Feldmäuse werden von Cosinus gefangen, d.h. der Anteil aller Mäuse, die Feldmäuse sind UND von Cosinus gefangen werden beträgt: 0,25·0,40=0,1
Den Rest der Einträge kann man nun recht einfach errechnen.

Wieviel Prozent der Spitzmäuse werden von Mathilde gefangen?
75% aller Mäuse sind Spitzmäuse. Spitzmäuse, die von Mathilde gefangen werden, machen einen Anteil von 50% aus.
Also fängt Mathilde einen Anteil von  der Spitzmäuse.
der Spitzmäuse.


