Oberstufe
W.20 | Konfidenzintervall, Hypothesentest (Irrtumswahrscheinlichkeit)
Eines der wichtigen Themen in der Schule ist derzeit der Hypothesentest
bzw. die Irrtumswahrscheinlichkeit. Dabei geht es um die Frage, ob es
Zufall ist oder nicht, wenn man bei einem Experiment einen Wert erhält,
der sehr weit vom Erwartungswert entfernt ist. Die folgenden Kapitel
über Konfidenzintervalle dienen der Vorbereitung auf die Kapitel:
„Hypothesentest/Irrtumswahrscheinlichkeit“.
Kriegen Sie bitte keinen Schreck, wenn Sie die Länge dieses Kapitels sehen.
Es gibt nämlich drei gängige Methoden, nach denen man die Hypothesentest-Aufgaben rechnen kann. In diesem Kapitel sind alle drei aufgeführt.
Sie brauchen nur eine dieser Methoden, also auch nur ein Drittel dieses Kapitels.
Teil A) W.20.01–W.20.04: Hier erfolgen alle Berechnungen mit GTR / CAS [grafischer Taschenrechners bzw. Computerprogramm]
Hinweis: Eine übersichtliche Bedienungsanleitung der gängigsten GTR/CAS finden Sie im Downloadcenter
Teil B) W.20.05–W.20.08: Gleiche Aufgaben, aber Berechnung über den klassischen Weg, also über den Umweg der Standard-Normal-Verteilung.
Hinweis: Die Tabellenwerte finden Sie am Ende des Kapitels „W.18 Normalverteilung“ oder im Downloadcenter
Teil C) W.20.09–W.20.12: Gleiche Aufgaben, aber Berechnung über die Tabellen der Binomialverteilung.
Hinweis: Die Tabellenwerte der Binomialverteilung finden Sie in vielen Büchern oder im Downloadcenter
In der Hypothesentest-Aufgabe geht es um Folgendes:
Für jedes Ereignis hat man eine bestimmte Wahrscheinlichkeit, mit der dieses eintrifft.
Nun ist es kein Geheimnis, dass es dadurch im Leben Situationen entstehen, die recht häufig eintreffen und andere Situationen, die eher selten eintreffen.
Beispiel:
Eine Münze zeigt mit einer W.S. von 50% Kopf und mit einer W.S. von 50% Zahl. Wenn man diese Münze nun 20 Mal wirft, wird es eher häufig vorkommen, dass man ca. 8, 9, 10, 11 oder 12 Mal "Kopf" erhält. Es wird aber eher selten vorkommen, dass man nur 3 Mal Kopf erhält oder 18 Mal Kopf.
Beim Hypothesentest interessiert man sich nun für die seltenen Ereignisse.
Speziell versucht man zu entscheiden, ob es einfach nur Pech war, wenn eines dieser Ereignisse eintrifft, oder ob die anfangs genannte W.S. falsch war.
Beispiel:
Unsere Münze wird 20 Mal geworfen. Normalerweise erwartet man in der Hälfte aller Fälle das Ereignis „Kopf“ [und in der anderen Hälfte der Fälle „Zahl“].
Nun fällt jedoch nur sechs Mal „Kopf“. Was bedeutet das? Hat man nur Pech gehabt, weil so selten Kopf dran kam, oder ist die Münze verbeult?
Man muss entscheiden, ob die Münze verbeult ist oder nicht.
Egal, wie man sich entscheidet, kann man immer falsch liegen.
Die Frage nach der Verbeultheit der Münze lässt sich also nicht mit „Richtig“ oder „Falsch“ beantworten, sondern nur:
Mit einer bestimmten W.S. richtig bzw. mit einer bestimmten W.S. falsch.
Der Ablauf ist ungefähr folgendermaßen:
Man hat eine Binomialverteilung oder eine Normalverteilung gegeben [bzw. sämtliche Abgaben, die man dafu?r braucht]. Beide haben die Form einer Glockenkurve [der Unterschied liegt nur darin, dann es in der Binomialverteilung nur einzelne Werte bzw. Balken gibt, in der Normalverteilung ist die Kurve durchgezogen].
1. In der Aufgabenstellung ist eine Wahrscheinlichkeit gegeben. Mit dieser und mit der Gesamtanzahl der Durchfu?hrungen [ist ebenfalls immer gegeben] berechnet man den Erwartungswert [E(x)=n·p]. Der Erwartungswert ist eigentlich nie gefragt, ist aber doch recht hilfreich.
2. Man hat in jeder Aufgabe eine Irrtumswahrscheinlichkeit gegeben. Das ist die Wahrscheinlichkeit des gesamten seltenen bzw. unwahrscheinlichen Bereiches.
Aus dieser Irrtumswahrscheinlichkeit berechnet man sich den Bereich, bzw. die linke und rechte Grenze des Hauptbereichs.
Man berechnet im Hypothesentest also keine W.S., sondern man berechnet die Grenzen von Intervallen.
3. Noch ein paar Kleinigkeiten, die man angeben oder berechnen muss. Ab dieser Stelle nicht mehr kompliziert.
Begriffe:
Der mittlere Bereich mit den häufig auftretenden Fällen heißt: „Annahmebereich“ oder „Konfidenzintervall“ oder „Vertrauensintervall“.
Die beiden äußeren Randbereiche mit den selten auftretenden Fällen heißen: Der „Ablehnungsbereich“.
Die W.S. des „Ablehnungsbereiches“ heißt „Irrtumswahrscheinlichkeit“ oder „Signifikanzniveau“ und wird eigentlich immer mit „α“ bezeichnet.
[Streng genommen ist die W.S. des Ablehnungsbereiches immer kleiner als „α“. Darauf gehen wir aber später noch einmal ein.]
Am Anfang der Aufgabe ist immer eine Wahrscheinlichkeit fu?r das Ereignis angegeben [bei der Mu?nze: p=0,6. Beim Wu?rfel: p=1/6].
Die Vermutung, dass diese Wahrscheinlichkeit stimmt, ist die Ausgangshypothese und heißt „Nullhypothese“ und wird mit H0 bezeichnet.
Die Gegenhypothese [also, dass p nicht stimmen wu?rde] heißt schlauer Weise „Gegenhypothese“ oder „Alternativhypothese“ und heißt H1.
Einen „Fehler 1.Art“ oder ein „α-Fehler“ begeht man, wenn man die Nullhypothese ablehnt (die in Wahrheit jedoch richtig ist) und die Gegenhypothese annimmt. Die W.S. so einen Fehler zu begehen, ist die W.S. des Ablehnungsbereiches.
Einen „Fehler 2.Art“ oder einen „β-Fehler“ begeht man, wenn man die Nullhypothese annimmt (die in Wahrheit jedoch falsch ist) und die Gegenhypothese ablehnt. Die W.S. so einen Fehler zu begehen, läßt sich nur schwer berechnen und ist daher so gut wie nie gefragt.

Obige Skizze zeigt die Skizze fu?r einen beidseitigen Hypothesentest. „Beidseitig“ deswegen, weil an beiden Enden der unwahrscheinlichste Rand weggeschnitten ist.
Im einseitigen Test ist nur einer der beiden Ränder abgeschnitten.
Im linksseitigen Hypothesentest der linke Rand, im rechtsseitigen Hypothesentest ist es der rechte Rand. [Details sehen wir in den folgenden Kapiteln.]

Bemerkung zur oberen Begrenzung der schraffierten Flächen:
Die durchgezogene Linie gehört zur Normalverteilung [die ist stetig, erlaubt also alle Nachkommastellen]. Die einzelnen Balken gehören zur Binomialverteilung [da gibt es nur Werte für ganze Zahlen]. Fu?r die Theorie des Hypothesentest ist es aber völlig wurst, ob es sich um Binomial- oder Normalverteilung handelt.
W.20.01 | beidseitige Konfidenzintervalle (über GTR bzw. CAS)
Intervallberechnungen [d.h: dieses Kapitel] ist an und für sich nicht wichtig.
Es dient „nur“ als Vorbereitung [fu?r Kap W.20.03], um die Grundlagen zu verstehen.
Im Prinzip machen wir hier sehr einfach Berechnungen: wir geben ein oder zwei Grenzen an und berechnen die W.S. dazwischen.
Zur Taschenrechnereingabe:
Sie werden immer wieder den Befehl fu?r die sogenannte „kumulierte Binomialverteilung“ brauchen, d.h. die Summe aller Wahrscheinlichkeiten, die bei „0“ anfängt und bei einer gewünschten Zahl „k“ aufhört. Ein GTR oder CAS [=grafischer Taschenrechner] hat einen eigenen Befehl dafu?r.
Beim GTR von Texas Instruments lautet der Befehl: „binomcdf()“. Sie finden den Befehl [je nach GTR-Modell] vermutlich unter „2nd“+„Distr“ „binomcdf(“ → oder im Katalog.
Die Eingabe erfolgt folgendermaßen: binomcdf(n,p,k)
Beim GTR von Casio lautet der Befehl: „BCD“. Sie wechseln in „STAT“-Menu?. Der Befehl „BCD“ kann nur auf Listen sinnvoll angewendet werden. Also erstellen
Sie sich eine Liste. Dazu markieren Sie einen gewünschten Listennamen [mit dem Cursor] und verwenden die Tastenkombination „OPTN“ → „F1“ [=„List“] → „F5“ [=„Seq“]. Hinter der Anzeige „Seq(“ geben Sie ein: „X,X,1,100,1“ ←„100“ ist die Zahl, bei welcher die Liste endet. Statt „100“ können Sie jede beliebige Zahl
eingeben. Nachdem die Liste erstellt ist, rufen Sie die Tastenkombination auf: „DIST“ [irgendwo oben, bei den „F1“–„F6“–Tasten] → „F5“ [=„BINM“] → „F2“ [=„Bcd“]. Unter „Numtrial“ geben Sie die Gesamtanzahl „n“ ein, unter „p“ natu?rlich die W.S.
Die „EXE“–Taste startet die Berechnung, die Ergebnisse erscheinen als Liste.
Beim CAS von TI lautet der Befehl: „binomcdf()“. Man kann den Befehl in einem Katalog finden oder einfach eingeben.
Die Eingabe erfolgt folgendermaßen: binomcdf(n,p,Startwert,Endwert).
[Der Startwert muss also nicht unbedingt „0“ sein].
Beim CAS von Casio lautet der Befehl: „binomialCDf()“. Man kann den Befehl in einem Katalog finden oder einfach eingeben.
Die Eingabe erfolgt folgendermaßen: binomialCDf(n,p,Startwert,Endwert).
Beispiel a.
Eine Größe ist binomialverteilt mit n=200 und p=0,25.
Sollte das Experiment eine Trefferhäufigkeit von u?ber 55 oder unter 40 liefern, so ist alles ganz furchtbar schlimm: das Universum kollabiert auf einen einzigen
unendlich kleinen Punkt und wir werden alle, in der Negativ-Unendlichkeit gefangen, sterben.
Mit welcher W.S. ist alles gut und wir sind gerettet?
Lösung:
Wenn man die unnu?tzen Informationen [mit dem Kollaps des Universums] weglässt, so ergibt sich folgende Sachlage: es du?rfen nicht mehr als 55 und nicht weniger als 40 Treffer auftreten. Wir brauchen also folgende W.S.: P(40<x<55) = P(40)+P(41)+P(42)+...+P(55)
Der mathematische Teil ist damit abgehakt, nun stellt sich nur noch die Frage, wie man das berechnet.
1. die mathematische Methode:
[Nach wenigen Stunden werden Sie mit dem Tippen fertig sein. ⇒ umständliche Methode]
2. die praktische Methode über den GTR/CAS
Wir brauchen den Befehl fu?r die kumulierte Binomialverteilung.
[Je nach GTR/CAS–Modell lautet der „binomcdf(“, „BCD“, „binomialCDf(“ oder ähnlich].
[Eine kurze Übersicht u?ber die Befehle finden Sie direkt oben vor Beispiel a. oder im Download-Center unter: „Bedienungsanleitung fu?r den GTR].
Normalerweise berechnen der GTR nur W.S., die bei „0“ beginnen und bis irgendwo hin gehen. Hier beginnt man jedoch bei 40. Das ist blöd.
Also berechnen wir die W.S. die bei „0“ beginnt und bei „55“ endet und ziehen vom Ergebnis die W.S. ab, die bei „0“ beginnt und bei „39“ endet.
Dann bleiben die Zahlen von „40“ bis „55“ u?brig.
Die Eingaben in Ihren GTR/CAS sollten sein:
GTR von TI: „binomcdf(200,0.25,55)–binomcdf(200,0.25,39)“
GTR von Casio: Liste programmieren, Werte bei „55“ und „39“ ablesen und voneinander abziehen.
CAS von TI: „binomcdf(200,0.25,55)–binomcdf(200,0.25,39)“ oder einfach „binomcdf(200,0.25,40,55)“
CAS von Casio: „binomialCDf(200,0.25,55)–binomialCDf(200,0.25,39)“
Zwischenergebnisse:
Fu?r die W.S. aller Zahlen von 0 bis 39 sollten Sie 0,041 erhalten.
Fu?r die W.S. aller Zahlen von 0 bis 55 sollten Sie 0,816 erhalten.
Fu?r die W.S. aller Zahlen von 40 bis 55 sollten Sie 0,775 erhalten.
⇒ P(40<x<55) = 0,775 ? 77,5%.
Beispiel b. [Lösung über GTR/CAS]
Heinz ist Nachtwächter in einem Parkhaus. Täglich macht er eine Strichliste u?ber die Automarken, die ein- und ausfahren. In jeder Schicht kommt er auf ca. 150
Auto die ein- und ausfahren. Angeblich sind 20% aller Fahrzeuge von der Firma VW. Um das zu überprüfen, sortiert Heinz die Listeneinträge in der Reihenfolge der Häufigkeit von VW. Diejenigen 10%, die am seltensten auftauchen, sind vermutlich Ausreißer, die will er nicht berücksichtigen.
Welche Anzahlen von VW werden auf den Listen übrig bleiben?
Lösung:
Eigentlich sind wir hier schon ziemlich in der Denkweise vom Hypothesentest drin. Wir verwenden nur die dementsprechenden Begriffe nicht. Nun zur Aufgabe:
Da jeden Tag 150 Fahrzeuge gezählt werden, von denen 20% VWs sein sollen, erwarten wir im Schnitt μ=150·0,2=30 VWs.
Die Zahl 30 sollte daher auch am häufigsten auftauchen.
Die Zahlen 29 und 31 sollten etwas seltener auftauchen,
die Zahlen 28 und 32 noch seltener, usw.
Am seltensten sollte der Fall 0-mal VW und der Fall 150-mal VW auftauchen.
Da Heinz die seltensten 10% aussortieren will, wäre es sinnvoll an beiden Enden der Skala jeweils 5% zu ignorieren, also da wo am wenigsten VW auftauchte [0; 1; 2; …] und da wo am häufigsten VW auftauchte [150; 149; 148; …].
Noch eine Bemerkung zu den 10%: de facto kommt man nie genau auf 10% [bzw. zwei Mal 5%]. Je nach gewählter Zahl kommt man entweder auf etwas mehr oder etwas weniger als 10%. In dieser Aufgabe wurde nichts präzisiert, aber in den typischen Hypothesentest-Aufgaben sucht man sich immer die Zahl aus, die
eine Prozentzahl liefert, die am nächsten unterhalb von 10% liegt. Nur deswegen werden wir auch hier die Ergebnisse so wählen, dass links und rechts
knapp unter 5% rauskommen werden.
Der linke unwahrscheinlichste Bereich [linker Ablehnungsbereich]:
Wir nehmen den Taschenrechner und lassen uns eine Wertetabelle der kumulierten W.S. anzeigen [d.h. je nach GTR/CAS-Modell sind das die Befehle: „binomcdf()“ bzw „BCD“]. Die Frage ist nun, welcher Wert die höchste W.S. liefert, die allerdings noch unter 5% liegt.
Der größte Wert bei dem die Summe aller W.S. noch unter 5% liegt, ist x=21.
Der linke unwahrscheinliche Bereich beginnt bei „0“ und endet bei „21“.
Heinz wird alle Tage, an welchen er 21 oder weniger VW gezählt hat, streichen, weil die extrem selten sind und als Ausreißer behandelt werden.
Der rechte unwahrscheinlichste Bereich [rechter Ablehnungsbereich]:
Wir betrachten wieder die Wertetabelle des Taschenrechners und pru?fen, welcher Wert die kleinste W.S. liefert, die allerdings bereits u?ber 95% liegt. [Die 95% deswegen, weil ich 95% erhalte, wenn ich von 100% die 5% abziehe]. Der kleinste Wert, bei dem die Summe aller W.S. u?ber 95% liegt, ist x=38.
Der rechte unwahrscheinliche Bereich beginnt bei „39“ und endet bei „150“.
Heinz wird also auch alle Tage, an welchen er 39 oder mehr VW gezählt hat, streichen, weil die ebenfalls extrem selten sind und als Ausreißer behandelt werden.
Antwort: Auf Nachtwächter Heinz´ toller Liste bleiben alle Tage übrig, an welchen eine Anzahl von 22 bis 38 Fahrzeuge der Marke VW gezählt wurden.
W.20.02 | einseitige Konfidenzintervalle (über GTR bzw. CAS)
Auch für dieses Kapitel gilt, dass dessen Sinn darin besteht, ein gute Vorbereitung für den Hypothesentest zu sein. Streng genommen, sind alle Aufgaben sogar Hypothesentest-Aufgaben, nur dass wir keinen der typischen Begriffe verwenden.
Beispiel c.
Robert plant eine lange Island-Tour. Zur Verpflegung nimmt er einen großen Vorrat an Müsli mit. Laut Hersteller sind mindestens 10% aller enthaltenen Nu?sse Paranüsse. Natu?rlich pru?ft Robert das nach [Robert prüft so was immer nach]. Aus irgend einer Packung entnimmt er 150 Nüsse und zählt nach.
a) Mit welcher W.S. findet er maximal 4 Paranüsse?
b) Mit welcher W.S. findet er weniger als 20 Paranüsse?
c) Die W.S. höchstens k Paranüsse zu finden, liegt bei mindestens 99%.
Welchen Wert hatte k?
Lösungen:
Bei der Aufgabe handelt es sich um eine Binomialverteilung. Die Gesamtanzahl der Versuche liegt bei n=150. Die W.S. fu?r einen Treffer [Paranuss] beträgt p=10%.
Es gibt nur zwei Ausgangsmöglichkeiten: entweder eine Paranuss oder eben nicht.
a) „Maximal drei Paranüsse“ setzt sich aus fu?nf Fällen zusammen: Null, eine, zwei drei oder vier Paranüsse. Mathematisch schreibt man das so:
P(x<3) = P(x=0)+P(x=1)+P(x=2)+P(x=3)+P(x=4)
1. die mathematische Methode:
Jeden der vier Fälle könnte man als Binomialverteilung ausrechnen.
2. die praktische Methode u?ber den GTR/CAS:
Wir brauchen den Befehl fu?r die kumulierte Binomialverteilung, denn wir brauchen die Summe aller W.S., die bei „0“ beginnen und bei „3“ enden.
Die Eingaben in Ihren GTR/CAS sollten sein:
GTR von TI: „binomcdf(150,0.1,4)“
GTR von Casio: Liste programmieren, Wert bei „4“ ablesen
CAS von TI: „binomcdf(150,0.1,4)“
CAS von Casio: „binomialCDf(150,0.1,4)“
Als Ergebnis sollten sie P(x<4) ≈ 0,00054 = 0,054% erhalten.
b) „Weniger als 20 Paranüsse“ ist eigentlich genau der gleiche Fall, wie in Teilaufgabe a), nur dass die gesuchte Zahl nicht mehr die „4“ ist, sondern „19“.
(Beachten Sie, dass „weniger als 20“ nicht „20“ ist, sondern „19“).
GTR von TI: „binomcdf(150,0.1,19)“
GTR von Casio: Liste programmieren, Wert bei „19“ ablesen
CAS von TI: „binomcdf(150,0.1,19)“
CAS von Casio: „binomialCDf(150,0.1,19)“
Sie sollten als Ergebnis P(x<20) ≈ 0,887 = 88,7% erhalten.
c) Im Prinzip haben wir mit der W.S. 99% das Endergebnis erhalten.
Die W.S. fu?r höchstens „k“ Paranüsse wird angegeben als: P(x<k)<99%
Wir tippen also die [kumulierte] Binomialverteilung in den GTR/CAS ein und „probieren einfach mal rum“, bis das Endergebnis bei knapp unter 99%=0,99 liegt.
GTR von TI: Wir geben den Befehl im y-Editor als Funktion ein: „y1=binomcdf(150,0.1,X)“. Nun schauen wir uns die Ergebnisse in der Wertetabelle an.
GTR von Casio: Liste programmieren, Ergebnisse angucken.
CAS von TI: Am einfachsten den Befehl als Funktion in der Wertetabelle eingeben [Grafikmenu?]: „f(x)=binomcdf(150,0.1,X)“.
CAS von Casio: Am einfachsten den Befehl als Funktion in der Wertetabelle eingeben [Grafikmenu?]: „f(x)=binomialCDf(150,0.1,X)“
Sie betrachten nun die y-Werte aus der Wertetabelle [welches die W.S. sind] und schauen nun einfach, welches die W.S. von ca 0,99 erscheint.
Fu?r x=23 erhalten Sie ein Ergebnis von unter 0,99 (y=0,986),
fu?r x=24 erhalten Sie ein Ergebnis von u?ber 0,99 (y=0,992).
Da nach dem x-Wert gefragt war, der eine W.S. von mindestens 99% liefert, ist die „24“ unser gesuchtes Ergebnis.
Antwort: Die W.S. von höchstens 24 Paranüssen liegt bei knapp über 99%.
Beispiel d.
Sarah L. ist Kinderkrankenschwester. In ihrer Ausbildung hat sie gelernt, dass höchstens jedes sechste Kind ein Frühgeborenes ist. Nun arbeitet sie auf einer Station, die 75 Neugeborene aufnehmen kann, davon 15 Frühgeborene.
a) Mit welcher W.S. hat sie zu einem Zeitpunkt so viele Frühchen auf der Station, dass die Ausstattung nicht ausreicht?
b) Fu?r wieviel Frühgeborene mu?sste die Ausstattung ausgelegt sein, damit sie bei 75 Geburten in höchstens einem von Tausend Fällen nicht ausreicht?
Lösungen
a) Wir brauchen im Prinzip die W.S., dass plötzlich 16 Fruhgeburten oder mehr auf der Station landen, also P(<16).
1. die mathematische Methode:

2. die praktische Methode über den GTR/CAS
Wir brauchen den Befehl fu?r die kumulierte Binomialverteilung.
[Je nach GTR/CAS–Modell lautet der „binomcdf(“, „BCD“, „binomialCDf(“ oder ähnlich].
[Eine kurze Übersicht u?ber die Befehle finden Sie oben vor Beispiel a. oder im Download-Center unter: „Bedienungsanleitung fu?r den GTR].
Normaler Weise berechnen der GTR nur W.S., die bei „0“ beginnen und bis irgendwo hin gehen. Hier beginnt man jedoch bei 16. Das ist blöd.
Also berechnen wir die W.S. die bei „0“ beginnt und bei „15“ endet und ziehen diese von 100%.
Erst mal die W.S. aller Werte von „0“ bis „15“ berechnen lassen:
GTR von TI: „binomcdf(75,1/6,15)“
GTR von Casio: Liste programmieren, Wert bei „15“ ablesen
CAS von TI: „binomcdf(75,1/6,15)“
CAS von Casio: „binomialCDf(75,1/6,15)“
Sie sollten P(x<15)≈0,825 erhalten. ⇒ P(X<16)=1–0,825=0,175=17,5%.
b) Wenn die Ausstattung in höchstens einem von 1000 Fällen nicht ausreicht, entspricht das einer W.S. von 1/1000 = 0,001. Umgekehrt bedeutet das, dass mit einer W.S. von mindestens 1–0,001 = 0,999 die Ausstattung ausreicht.
.png)
Bei welcher Anzahl von Frühchen reicht die Ausstattung wohl aus?
Na ja, die untere Grenze ist einfach: x1=0 [wenn´s kein Frühchen hat, reicht ja jede Ausstattung aus]. Die obere Grenze suchen wir.
Wir tippen also die [kumulierte] Binomialverteilung in den GTR/CAS ein und „probieren einfach mal rum“, bis das Endergebnis bei knapp u?ber 0,999 liegt.
GTR von TI: Wir geben den Befehl im y-Editor als Funktion ein: „y1=binomcdf(75,1/6,X)“. Nun schauen wir uns die Ergebnisse in der Wertetabelle an.
GTR von Casio: Liste programmieren, Ergebnisse angucken.
CAS von TI: Am einfachsten den Befehl als Funktion in der Wertetabelle eingeben [Grafikmenu?]: „f(x)=binomcdf(75,1/6,X)“.
CAS von Casio: Am einfachsten den Befehl als Funktion in der Wertetabelle eingeben [Grafikmenu?]: „f(x)=binomialCDf(75,1/6,X)“
Sie erhalten nun ein Liste von y-Werten [welches die W.S. ist] und schauen nun einfach, bei welchem x-Wert die W.S. von knapp u?ber 0,999 erscheint.
Für x=23 erhalten Sie erstmalig ein Ergebnis von u?ber 0,999 (y=0,9991).
Der Annahmebereich ist [0;23]. Der Ablehungsbereich also [24;75].
Antwort: Wenn die Station fu?r 23 Frühchen ausgestattet ist, reicht das wahrscheinlich in weniger als 1 von 1000 Fällen nicht aus.
W.20.03 | beidseitige Hypothesentests (GTR bzw. CAS)
[Die Grundbegriffe zum Hypothesentest finden Sie oben am Anfang des Kapitels.]

Beispiel e.
Bei einem Konzert der Band „Under Rieten“ sind üblicher Weise ein Drittel der Besucher im Alter zwischen 40 und 49 Jahren [kurz: Vierziger].
Nach Erscheinen des Albums „Feuchtträume des schönen Zwergwiesensalamanders“ soll nun überprüft werden, ob sich die Altersstruktur der Fangemeinde in irgendeiner Weise geändert hat. Eine Umfrage unter 150 Personen ergibt, dass 40% zu den Vierzigern gezählt werden können.
a) Formulieren Sie die Nullhypothese H0 und die Alternativhypothese H1.
b) Können die Bandmitglieder von „Under Rieten“ mit einer Irrtumswahrscheinlichkeit von α=5% davon ausgehen, dass sich die Alterverteilung geändert hat?
c) Bestimmen Sie den Fehler 1.Art (α-Fehler).
Lösungen:
a) Die Nullypothese H0 ist die Theorie, dass die Wahrscheinlichkeit, die in der Aufgabe formuliert war (also ein Drittel), stimmt.
In Worten: H0 ist die Hypothese, dass ein Drittel der Besucher „Vierziger“ sind.
H1 ist die Annahme, dass nicht ein Drittel der Besucher „Vierziger“ sind.
b) Normalerweise erwartet man, dass von den 150 befragten Personen ein Drittel zu den Vierzigern gehören, also 50 Personen.
Nun sind es jedoch 40% von 150, also 60 Personen und damit stellt sich die Frage, ob der Anteil in Wahrheit immer noch bei einem Drittel liegt und nur an
diesem Abend etwas mehr Vierziger kamen, oder ob die W.S. prinzipiell mehr als ein Drittel geworden ist. Das zu beantworten, ist unser Ziel.
Einen Hypothesentest geht man nicht so an, dass man sagt: „Mit welcher W.S. tauchen u?berhaupt 60 Vierziger auf“, sondern man fragt: bis zu welcher Zahl sagt man: „60 Vierziger sind heute einfach nur Zufall“ und ab welcher Zahl sagt man: „Die W.S. von ein Drittel stimmt nicht mehr“.
Man u?berlegt: „Welches sind die unwahrscheinlichsten 5%, die auftreten könnten?“ [5% deswegen, weil in dieser Aufgabe die Irrtumsw.s. bei α=5% liegt].
Danach überprüft man einfach, ob die gegebene Anzahl [hier die 60 Personen] in diesem unwahrscheinlichen Bereich liegen oder nicht.
α=5% teilen wir uns auf, in die 2,5% mit den kleinsten unwahrscheinlichen Werten [also dass 0,1,2,... Vierziger auftauchen] und 2,5% mit den größten unwahrscheinlichen Werten [dass also 150, 149, 148, … Vierziger auftauchen].
Das untere 2,5%-Intervall: Wir denken uns eine Binomialverteilung mit n=150 und p=1/3. Nun lassen Sie sich vom GTR eine Liste mit der kumulierten Binomialverteilung angeben [GTR-Befehl „binomcdf(“ oder „BCD“ oder „binomialCDf(“ oder ...] und schauen nun, bis zu welchem x-Wert die W.S. noch unter 0,025 liegt. Dieses sollte beim x-Wert „38“ der Fall sein.

Da die Grenze des oberen 2,5%-Intervalls gleichzeitig auch die Grenze des unteren 97,5%-Intervalls ist, berechnen wir dieses. Sie schauen abermals auf die Wertetabelle des GTR und suchen denjenigen x-Wert, dessen W.S. erstmalig u?ber 0,975 liegt. Dieses sollte bei „61“ der Fall sein.
Jetzt wissen wir alles, was wir wissen mu?ssen: Es ist sehr unwahrscheinlich, dass eine Anzahl von Vierzigern auftaucht, die zwischen 0 und 38 oder von 62 bis 150 liegt [„unwahrscheinlich“ heißt: 5% oder weniger].
Eine Anzahl von 39 bis 61 Vierzigern ist wahrscheinlicher [„wahrscheinlicher“ heißt: 95% oder mehr]. Da beim „Under Rieten“-Konzert eine tatsächliche Anzahl von 60 Vierzigern auftrat, liegt das noch im wahrscheinlichen Bereich.
Anders formuliert: Bei einer angenommenen W.S. von p=1/3, wäre es noch denkbar, dass 60 Vierziger auftauchen. Die Altersstruktur der Fangemeinde von „Under Rieten“ hat sich auch nach dem Album „Feuchtträume des schönen
Zwergwiesensalamanders“ eher nicht geändert.
Fachlich gesprochen, haben wir die Nullhypothese angenommen.
c) Der Fehler 1.Art ist die Wahrscheinlichkeit des Ablehnungsbereiches.


Beispiel f.
Ein Hotel im griechischen Matala beherrbergt durchschnittlich 75% deutsche Touristen [die abends Brot essen] und 25% griechische Touristen [die abends kein Brot essen]. Andere Nationalitäten sind vernachlässigbar. Nach einer Umbaumaßnahme will der Hotelchef pru?fen, ob sich der Anteil der Nationalitäten verschoben hat [das ist wichtig, denn wenn´s mehr Deutsche gibt, muss er mehr Brot kaufen, gibt’s weniger Deutsche muss er weniger Brot kaufen]. Dafu?r lässt er eines Abends einen Praktikanten die 200 Hotelgäste durchzählen.
Der Praktikant zählt 138 Deutsche.
a) Formulieren Sie die Nullhypothese H0 und die Alternativhypothese H1.
b) Kann mit einer Irrtumswahrscheinlichkeit von 10% davon ausgegangen werden, dass sich der Anteil der Deutschen geändert hat?
c) Bestimmen Sie den Fehler 1.Art (α-Fehler).
Lösungen:
a) Die Nullhypothese H0 ist die Annahme, dass 75% der Touristen Deutsche sind.
Die Alternativhypothese H1 ist die Annahme, dass nicht 75% der Touristen Deutsche sind.
kurz: H0 : p=0,75 H1 : p≠0,75
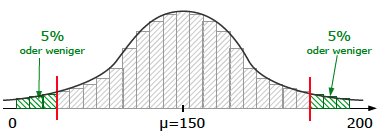
b) Wir fangen hinten an. Eine Irrtumswahrscheinlichkeit von 10% bedeutet, dass wir links und rechts von der Verteilung jeweils die seltensten 5% abschneiden.
[Es handelt sich natu?rlich um einen beidseitigen Hypothesentest, denn sowohl wenn´s zu viele, als auch wenn´s zu wenig Deutsche sind, wäre die Situation geändert.]
Die Zahl „138“ lassen wir komplett weg, die brauchen wir erst ganz zum Schluss. Die Rechnung erfolgt u?ber eine Binomialvert. mit n=200 und p = 75% = 0,75. Wir nehmen unseren GTR oder CAS zur Hand und lassen uns eine Liste mit der kumulierten W.S. anzeigen. Wir mu?ssen zwei Grenzen ablesen.
Einerseits die untere Grenze bei 5%?0,05, andererseits die obere Grenze bei 95%?0,95 [95% daher, weil der Taschenrechner mit der Rechnung immer links, bei Null, beginnt. Und wenn sich oberhalb der Grenze 5% befinden, sind sich unterhalb der Grenze 100%– 5%=95%].
Untere Grenze: welcher x-Wert ist der letzte, dessen W.S. noch unter 0,05 liegt? Laut Liste ist das bei x=139 der Fall.
Obere Grenze: welcher x-Wert ist der erste, dessen W.S. bereits u?ber 0,95 liegt? Laut Liste ist das bei x=160 der Fall.
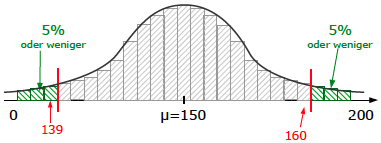
Der Ablehnungsbereich geht also von 0 bis 139 und von 161 bis 200. Der Annahmebereich liegt zwischen 140 und 160.
Jetzt erst kommt die Zahl von 138 gezählten Deutschen ins Spiel. Da diese Zahl im Ablehnungsbereich liegt, muss man davon ausgehen, dass die anfangs angenommene W.S. von 75% nicht stimmt.
Korrekte Formulierung: Die Zahl von 138 Deutschen liegt im Ablehnungsbereich. Daher wird die Nullhypothese [75% der Urlauber sind Deutsche] verworfen, die Gegenhypothese [nicht 75% der Urlauber sind Deutsche] wird angenommen. Diese Aussage wird mit einer Irrtumswahrscheinlichkeit [oder auch: auf einem Signifikanzniveau] von 10% getroffen.
Sollten wir falsch liegen [und es kommen tatsächlich immer noch 75% Deutsche ins Hotel], so hätten wir eine Fehler 1.Art begangen. Die W.S. davon berechnen wir jetzt.
c) Der Fehler 1.Art ist die Wahrscheinlichkeit des Ablehnungsbereiches.

W.20.04 | einseitige Hypothesentests (GTR bzw. CAS)
[Die Grundbegriffe zum Hypothesentest finden Sie oben am Anfang des Kapitels.]

Beispiel g.
Bei einer bestimmten Vogelart liegt der Anteil der Weibchen angeblich bei mindestens 60%. Ein Landschaftsgärtner zählt das nach. Bei 75 gezählten
Exemplaren kommt er auf 39 Weibchen.
a) Formulieren Sie die Nullhypothese H0 und die Alternativhypothese H1.
b) Kann die Häufigkeit von 60% mit einer Irrtumswahrscheinlichkeit von 6% aufrecht erhalten werden?
c) Bestimmen Sie den Fehler 1.Art (α-Fehler).
Lösungen:
a) Die Nullhypothese H0 ist die Annahme, dass mindestens 60% der Vögel weiblich sind. [Also 60% oder mehr].
Die Alternativhypothese H1 ist die Annahme, dass höchstens 60% der Vögel weiblich sind. [Also weniger als 60%].
b) Normalerweise erwartet man, dass von den 75 Vögeln mindestens 60% weiblich sind, also mindestens  = 45 Weibchen.
= 45 Weibchen.
Nun sind es jedoch nur 39, als zu wenig und damit stellt sich die Frage, ob der Anteil in Wahrheit weniger als 60% ist oder ob nur zufällig heute etwas weniger sind, ohne dass es eine besondere Bedeutung hätte.
Am Rechenweg des Hypothesentests ist ungewöhnlich, dass man das Ganze ru?ckwärts rechnet. Man könnte also folgende Rechnung aufstellen: 39 Weibchen von 75 Vögel sind .png) . Das ist ein ganz tolle Rechnung, die bringt aber nichts. Die tatsächliche Anzahl von 39 Weibchen, lässt man komplett weg, die kommt erst ganz zum Schluss.
. Das ist ein ganz tolle Rechnung, die bringt aber nichts. Die tatsächliche Anzahl von 39 Weibchen, lässt man komplett weg, die kommt erst ganz zum Schluss.
1. Man beginnt mit der Überlegung, ob es sich um einen rechts- oder linksseitigen Hypothesentest handelt. Dazu ist es zwar nicht notwendig, aber
hilfreich, den Erwartungswert zu berechnen. Der ist hier: E(x) = n·p = 75·60% = 45.
Es sollten mindestens 60% weiblich sein, also sollten mindestens 45 Weibchen darunter sein. Jede Anzahl u?ber 45 Weibchen wäre also akzeptabel. Nur wenn´s wesentlich weniger als 45 Weibchen wären, wäre das schlecht. Daher muss man das Ende am linken Rand abschneiden, es ist ein linksseitiger Test.
Faustregel [gilt nicht als richtig mathematische Begru?ndung]:
Ein linksseitiger Test liegt vor, wenn das Wort „mindestens“ verwendet wird, bzw. wenn der gegebene Wert [hier die Zahl von „39“] links vom
Erwartungswert liegt.
Ein rechtsseitiger Test liegt vor, wenn das Wort „höchstens“ verwendet wird, bzw. wenn der gegebene Wert [hier die Zahl von „39“] rechts vom
Erwartungswert liegt.
2. Aus der Irrtumswahrscheinlicheit α berechnet man die Grenze, bis zu welcher man die Hypothese [hier die W.S. von mindestens 60%] ablehnt oder annimmt. Man bemu?ht dazu die Wertetabelle des GTR mit der kumulierten Binomialverteilung [wie in Bsp.3 oder Bsp.4] und sucht die x-Werte, die zu den Wahrscheinlichkeiten passen.
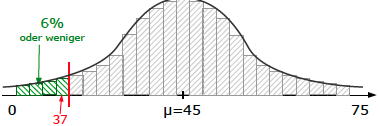
Beim linksseitigen Test sucht man den x-Wert, dessen (kumulierte) W.S. grad noch unter der W.S.
α=0,06 liegt. Dieser x-Wert ist die oberste Grenze des Ablehnungsbereiches.
Bei einem rechtsseitigen Test wu?rde man jenen x-Wert suchen, dessen (kumulierte) W.S. gerade noch u?ber der W.S. 1–α=0,94 liegt. Dieser x-Wert ist
die oberste Grenze des Annahmebereiches.
In unserer Aufgabe handelt es sich um einen linksseitigen Test, also suchen wir den höchsten x-Wert, dessen W.S. noch unter α=0,06 liegt.
Der GTR-Liste mit der kumulierten Binomialverteilung entnimmt man:
P(x<37)≈0,04 und P(x<38)≈0,064. Also ist x=37 die von uns gesuchte Zahl.
Wir wissen jetzt, dass die Zahlen „0“ bis „37“ den Ablehnungsbereich bilden [also den äußeren, linken Rand]. Die Zahlen „38“ bis „75“ bilden den
Annahmebereich [das Hauptfeld mit dem Erwartungswert drin].
3. Pru?fen, ob die gegebene Zahl [hier die „39“] im Ablehnungs- oder im Annahmebereich liegt:
Am Anfang der Aufgabe war die Anzahl von 39 gezählten Weibchen gegeben.
Diese Zahl liegt im Annahmebereich. Die These „mindestens 60% Weibchen“ wird also angenommen [man geht davon aus, dass „mindestens 60%“ stimmen].
⇒ Es kann nicht ausgeschlossen werden, dass p=60% falsch ist.
⇒ Die Hypothese p=60% wird daher angenommen.
c) Der Fehler 1.Art ist die Wahrscheinlichkeit des Ablehnungsbereiches. Fehler ⇒ 1.Art = P([0;37]) = [GTR] ≈ 0,0395

Beispiel h.
Der bestaussehendste Gewinner der Fernsehshow „Germanys next Popp-Modell“ behauptet, dass höchstens 10% der Frauen ihm widerstehen können.
Um das zu u?berpru?fen wird er in ein Lokal eingeladen, in welchem sich 100 Frauen befinden. Von diesen fallen 16 Frauen nicht in Ohnmacht.
a) Formulieren Sie die Nullhypothese H0 und die Alternativhypothese H1.
b) Kann mit einer Irrtumswahrscheinlichkeit von 5% davon ausgegangen werden, dass die Angaben des Poppstars stimmen?
c) Bestimmen Sie den Fehler 1.Art (α-Fehler).
Lösung
a) H0: höchstens 10% der Frauen widerstehen dem Poppstar. [Also 10% oder weniger].
H1: mehr als 10% der Frauen können dem Poppstar widerstehen.
b) Handelt es sich um einen links- oder einen rechtsseitigen Test?
Der Mittelwert liegt bei μ=100·10%=100·0,1=10 Frauen die nicht widerstehen, die also nicht in Ohnmacht fallen sollten. Dummerweise sind es in Wirklichkeit 16. Das spricht dafu?r, dass die „Problemzone“ am rechten Rand ist. Also eine rechtsseitiger Test. Die W.S. von höchstens 10% spricht ebenfalls dafu?r.
Die Grenze zwischen Ablehnungs- und Annahmebereich: Da es sich um einen rechtsseitigen Test handelt, ist fu?r uns 1–α wichtig.
Wir nehmen unseren GTR/CAS und lassen uns fu?r n=100 und p=0,1 die Liste fu?r die kumulierte Binomialverteilung anzeigen. Nun suchen wir den größten x-Wert, dessen W.S. knapp über 1– = 1–0,05=0,95 liegt. P(x<14) liegt noch unter 0,95 und P(x<15) ist bereits größer als 0,95. Der Annahmebereich ist demnach das Intervall
[0;15], der Ablehnungsbereich ist das Intervall [16;100].

Vor dem Poppstar sind 16 Frauen nicht in Ohnmacht gefallen. „16“ befindet sich im Ablehnungsbereich, was dafu?r spricht, dass mehr als 10% der Frauen dem Poppstar widerstehen. Die Nullhypothese muss also abgelehnt werden.
c) Der Fehler 1.Art ist die Wahrscheinlichkeit des Ablehnungsbereiches.
Fehler 1.Art = P([16;⇒ 100]) 1–P([0;15]) = [GTR] 1–0,9601 ≈ 0,0399
W.20.05 | beidseitige Konfidenzintervalle (über Normalverteilung)
Beispiel a.
Eine Größe ist binomialverteilt mit n=200 und p=0,25.
Sollte das Experiment eine Trefferhäufigkeit von über 55 oder unter 40 liefern, so ist alles ganz furchtbar schlimm: das Universum kollabiert auf einen einzigen unendlich kleinen Punkt und wir werden alle, in der Negativ-Unendlichkeit gefangen, sterben. Mit welcher W.S. ist alles gut und wir sind gerettet?
Lösung:
Wenn man die unnützen Informationen [mit dem Kollaps des Universums] weglässt, so ergibt sich folgende Sachlage: es dürfen nicht mehr als 55 und nicht weniger als 40 Treffer auftreten. Eine vernünftige Rechenmethode liefert die Normalverteilung.
Für die Normalverteilung brauchen wir μ und σ.


Beispiel b.
Heinz ist Nachtwächter in einem Parkhaus. Täglich macht er eine Strichliste über die Automarken, die ein- und ausfahren. In jeder Schicht kommt er auf ca. 150 Autos die ein- und ausfahren. Angeblich sind 20% aller Fahrzeuge von der Firma VW. Um das zu überprüfen, sortiert Heinz die Listeneinträge in der Reihenfolge der Häufigkeit von VW. Diejenigen 10%, die am seltensten auftauchen, sind vermutlich Ausreißer, die will er nicht berücksichtigen.
Welche Anzahlen von VW werden auf den Listen übrig bleiben?
Lösung:
Eigentlich sind wir hier schon ziemlich in der Denkweise vom Hypothesentest drin. Wir verwenden nur die dementsprechenden Begriffe nicht.
Nun zur Aufgabe: Da jeden Tag 150 Fahrzeuge gezählt werden, von denen 20% VWs sein sollen, erwarten wir im Schnitt μ=150·0,2=30 VWs.
Die Zahl 30 sollte daher auch am häufigsten auftauchen. Die Zahlen 29 und 31 sollten etwas seltener auftauchen, die Zahlen 28 und 32 noch seltener, usw.
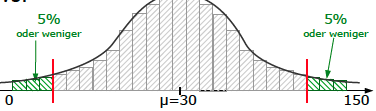
Am seltensten sollte der Fall 0-mal VW und der Fall 150-mal VW auftauchen.
Da Heinz die seltensten 10% aussortieren will, wäre es sinnvoll an beiden Enden der Skala jeweils 5% zu ignorieren, also da wo am wenigsten VW auftauchte [0; 1; 2; …] und da wo am häufigsten VW auftauchte [150; 149; 148; …].
Noch eine Bemerkung zu den 10%: de facto kommt man nie genau auf 10% [bzw. zwei Mal 5%]. Je nach gewählter Zahl kommt man entweder auf etwas mehr oder etwas weniger als 10%. In dieser Aufgabe wurde nichts präzisiert, aber in den typischen Hypothesentest-Aufgaben sucht man sich immer die Zahl aus, die eine Prozentzahl liefert, die am nächsten unterhalb von 10% liegt. Nur deswegen werden wir auch hier die Ergebnisse so wählen, dass links und rechts knapp unter 5% rauskommen werden.
Im Prinzip machen wir jetzt den gleichen Rechenweg, wie in Kapitel „W.18 Normalverteilung“ [Bsp.e, Bsp.g und Bsp.h], nur rückwärts.
Wir brauchen auf jeden Fall μ und σ.
μ = n·p = 150·0,2 = 30

Die Grenze zum linke unwahrscheinlichen Bereich [zum linker Ablehnungsbereich]:
Wir kennen erst mal nur die W.S. des gesamten linken Bereichs. Wir schlagen in der Tabelle nach, welcher z-Wert zu Φ=5%=0,05 gehört. Doch: Oh Nein! In der Tabelle gibt es nur W.S.-Werte von 0,5 bis 1. Der Trick: Wir schlagen die W.S. 1–0,05=0,95 nach und ändern vom erhaltenen z-Wert das Vorzeichen.
Φ=0,05 ⇒ Φ*=1–0,05=0,95 ⇒ [Tabelle] ⇒ z*≈1,645 ⇒ z=-1,645
Aus dem z-Wert berechnen wir den x-Wert:

Merken! - Eine linke Grenze wird immer abgerundet, um die linke Grenze des Annahmebereiches zu erhalten.
22,44 wird auf 22 abgerundet. Der Annahmebereich beginnt also bei 22!
Heinz wird also alle Tage, an welchen er 21 oder weniger VW gezählt hat, streichen, weil die extrem selten sind und als Ausreißer behandelt werden.
Die Grenze zum rechten unwahrscheinlichen Bereich [zum rechten Ablehnungsbereich]:
Wir kennen auch hier erst mal nur die W.S. des gesamten rechten Bereichs. Das ist aber ungeschickt, denn die Tabelle der Normalverteilung kann nicht mit Bereichen umgehen, die irgendwo anfangen und nach rechts gehen, sondern nur mit Bereichen, die irgendwo beginnen und nach links gehen.
Wenn der rechte Außenbereich die W.S. von Φ*=5% hat, so der ganze Rest eine W.S. von 100%–5%=95% ⇒ Φ=95%=0,95
Φ=0,95 ⇒ [Tabelle] ⇒ z≈1,645
Aus dem z-Wert berechnen wir den x-Wert:
Merken! - Eine rechte Grenze wird immer aufgerundet, um die rechte Grenze des Annahmebereiches zu erhalten.
37,56 wird auf 38 aufgerundet. Der Annahmebereich endet also bei 38!
Heinz wird also auch alle Tage, an welchen er 39 oder mehr VW gezählt hat, streichen, weil die ebenfalls extrem selten sind und als Ausreißer behandelt werden.
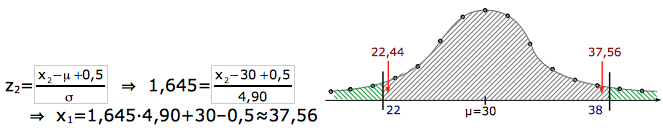
Antwort: Auf Nachtwächter Heinz´ toller Liste bleiben alle Tage übrig, an welchen eine Anzahl von 22 bis 38 Fahrzeuge der Marke VW gezählt wurden.
Beispiel c.
Robert plant eine lange Island-Tour. Zur Verpflegung nimmt er einen großen Vorrat an Müsli mit. Laut Hersteller sind mindestens 10% aller enthaltenen Nüsse Paranüsse. Natürlich prüft Robert das nach [Robert prüft so was immer nach]. Aus irgend einer Packung entnimmt er 150 Nüsse und zählt nach.
a) Mit welcher W.S. findet er maximal 4 Paranu?sse?
b) Mit welcher W.S. findet er weniger als 20 Paranu?sse?
c) Die W.S. höchstens k Paranüsse zu finden, liegt bei mindestens 99%. Welchen Wert hatte k?
Lösung
Es handelt sich hier um eine Binomialverteilung. Die Gesamtanzahl der Versuche liegt bei n=150. Die W.S. fu?r einen Treffer [=eine Paranuss] beträgt p=10%. Es gibt nur zwei Ausgangsmöglichkeiten: entweder eine Paranuss oder eben nicht. Diese Binomialverteilung wandeln wir in die Standardnormalverteilung um.
Für die Normalverteilung brauchen wir μ und σ.
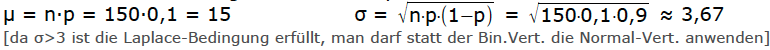
a) Für die Normalverteilung braucht man üblicher Weise zwei Grenzen. Bei der Fragestellung „Maximal drei Paranüsse“ ist die obere Grenze x2=4, die untere Grenze ist unausgesprochen x1=-∞ [oder x1=0, falls Ihnen das sympathischer ist].
Wir rechnen die Grenzen x1=-∞ und x2=4 in Grenzen der Standard-Normal- Verteilung um [bedenken Sie, dass bei der kleineren Grenze immer 0,5 abgezogen wird und bei der größeren Grenze immer 0,5 dazu gezählt wird].
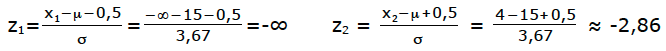
Aus der Tabelle der Standard-Normal-Verteilung entnimmt man die W.S.
[die Tabelle finden Sie am Ende von Kap. W.18 oder im Downloadcenter]
z1 = -∞ ⇒ Φ(-∞) = 0
z2 = -2,86 ⇒ Φ(-2,86) = 1–Φ(2,86) ≈ 1–0,998 = 0,002
Die gesuchte W.S. beträgt 0,0009–0 = 0,002 ? 0,2%.
b) „Weniger als 20 Paranüsse“ sind „19“. [Wir gehen ähnlich vor wie in Teilaufgabe a)]
Wir suchen also P(x<19). Die obere Grenze ist x2=19, die untere Grenze ist unausgesprochen x1=-∞ [oder x1=0]. Wir rechnen die Grenzen x1=-∞ und x2=19 in Grenzen der Standard-Normal-Verteilung um.
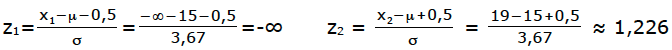
Aus der Tabelle der Standard-Normal-Verteilung entnimmt man die W.S.
z1 = -∞ ⇒ Φ(-∞) = 0 z2 = 1,226 ⇒ Φ(1,23) ≈ 0,890
Die gesuchte W.S. beträgt 0,89–0 = 0,89 ? 89%.
c) Im Prinzip haben wir mit der W.S. 99% das Endergebnis erhalten.
Die W.S. für höchstens „k“ Paranüsse wird angegeben als: P(x<k)>99%
Wir rechnen nun rückwärts. Da es um höchstens … Paranüsse geht, ist die untere Grenze x1=0. Wir brauchen also nur die obere Grenze.
Wir schnappen uns die Tabelle und schauen, welcher „z“-Wert zu Φ=0,99 gehört. Das ist ungefähr der Wert z=2,33. Nun rechnen wir den „z“-Wert [der Standard-Normal-Verteilung] in den „x“-Wert [der Binomialverteilung] um.
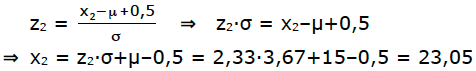
Da es mindestens 99% sein sollen, dürfen wir die 23,05 keinesfalls abrunden
[sonst werden es ja weniger als 99%], sondern wir runden auf 24.
Antwort: Die W.S. von höchstens 24 Paranüsse liegt bei knapp u?ber 99%.
Beispiel d.
Sarah L. ist Kinderkrankenschwester. In ihrer Ausbildung hat sie gelernt, dass höchstens jedes sechte Kind ein Frühgeborenes ist. Nun arbeitet sie auf einer Station, die 75 Neugeborene aufnehmen kann, davon 15 Frühgeborene.
a) Mit welcher W.S. hat sie zu einem Zeitpunkt so viele Frühchen auf der Station, dass die Ausstattung nicht ausreicht?
b) Für wieviel Neugeborene müsste die Ausstattung ausgelegt sein, damit sie bei 75 Geburten in höchstens einem von Tausend Fällen nicht ausreicht?
Lösung:
Bei der Aufgabe handelt es sich um eine Binomialverteilung. Die Gesamtanzahl der Versuche liegt bei n=75. Die W.S. für einen Treffer [=ein Fru?hgeborenes] beträgt p=1/6≈16,7%. Es gibt nur zwei Ausgangsmöglichkeiten: entweder ein Frühgeborenes oder eben nicht.
Diese Binomialverteilung wandeln wir in die Standardnormalverteilung um.
Für die Normalverteilung brauchen wir μ und σ.

a) Wir brauchen im Prinzip die W.S., dass plötzlich 16 Frühgeburten oder mehr auf der Station landen, also P(X?16). Die untere Grenze ist also x1=16, die obere Grenze ist unausgesprochen x2=∞ [oder x2=75, falls Ihnen das sympathischer ist].
Wir rechnen die Grenzen x1=16 und x2=∞ in Grenzen der Standard-Normal- Verteilung um [bedenken Sie, dass bei der kleineren Grenze immer 0,5 abgezogen wird und bei der größeren Grenze immer 0,5 dazu gezählt wird].
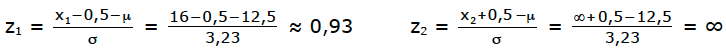
Aus der Tabelle der Standard-Normal-Verteilung entnimmt man die W.S.
[die Tabelle finden Sie am Ende von Kap. W.18 oder im Downloadcenter]
z1 = 0,93 ⇒ Φ(0,93) ≈ 0,824
z2 = ∞ ⇒ Φ(∞) = 1
Die gesuchte W.S. beträgt 1–0,824 = 0,176 ? 17,6%.
b) Wenn die Ausstattung in einem von 1000 Fällen nicht ausreicht, entspricht das einer W.S. von 1/1000=0,001. [In der Skizze: der rechte schraffierte Bereich].
Bei welcher Anzahl von Frühchen reicht die Ausstattung nicht aus?
Man geht am besten immer vom Hauptbereich aus, wir fragen also:
bei welcher Anzahl von Frühchen reicht die Ausstattung aus?
Die untere Grenze ist klar: wenn sehr wenig Fru?hchen da sind, ist’s problemlos.
Die untere Grenze ist also x1=-∞ [oder 0, falls Ihnen das lieber ist]. Die obere Grenze ist die Herausforderung dieser Aufgabe.
Wir rechnen nun rückwärts.
Wir schnappen uns die Tabelle und schauen, welcher „z“-Wert zu Φ=0,999 gehört. [Wir müssen mit 0,999 rechnen und nicht mit 0,001, denn die Tabelle ist immer für
Intervalle ausgelegt, die links beginnen und nicht rechts!].

Das ist ungefähr der Wert z=3,09. Nun rechnen wir den „z“-Wert [der Standard- Normal-Verteilung] in den „x“-Wert [der Binomialverteilung] um.
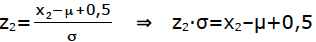
⇒ x2=z2·σ+μ–0,5 = 3,09·3,23+12,5–0,5 = 21,98
Da wir die rechte Grenze ausgerechnet haben, müssen wir immer aufrunden.
Die Anzahl der Frühgeborenen, bei denen die Ausstattung ausreicht, liegt also von 0 bis 22. Die Anzahl der Frühgeborenen, bei denen die Ausstattung nicht ausreicht, liegt also von 23 aufwärts.
Antwort: In weniger als 1 von 1000 Fällen gibt es 23 Frühchen. Ist also eine Ausstattung für höchstens 22 Frühchen vorhanden, reicht die Ausstattung in weniger als 1 von 1000 Fällen nicht aus.
W.20.07 | beidseitige Hypothesentests (über Normalverteilung)
Bei einem Konzert der Band „Under Rieten“ sind üblicher Weise ein Drittel der Besucher im Alter zwischen 40 und 49 Jahren [kurz: Vierziger].
Nach Erscheinen des Albums „Feuchtträume des schönen Zwergwiesensalamanders“ soll nun überprüft werden, ob sich die Altersstruktur der Fangemeinde in irgend einer Weise geändert hat. Eine Umfrage unter 150 Personen ergibt, dass 40% zu den Vierzigern gezählt werden können.
a) Formulieren Sie die Nullhypothese H0 und die Alternativhypothese H1.
b) Können die Bandmitglieder von „Under Rieten“ mit einer Irrtumswahrscheinlichkeit von α=5% davon ausgehen, dass sich die Alterverteilung geändert hat?
c) Bestimmen Sie den Fehler 1.Art (α-Fehler).
Die Lösungen und weitere Aufgaben findest du hier.
Verwandte Kapitel:
W.20 | Konfidenzintervall, Hypothesentest (Irrtumswahrscheinlichkeit)
- W.20.01 | beidseitige Konfidenzintervalle (über GTR bzw. CAS)
- W.20.02 | einseitige Konfidenzintervalle (über GTR bzw. CAS)
- W.20.03 | beidseitige Hypothesentests (GTR bzw. CAS)
- W.20.04 | einseitige Hypothesentests (GTR bzw. CAS)
- W.20.05 | beidseitige Konfidenzintervalle (über Normalverteilung)
- W.20.06 | einseitige Konfidenzintervalle (über Normalverteilung)
- W.20.07 | beidseitige Hypothesentests (über Normalverteilung)
- W.20.08 | einseitige Hypothesentests (über Normalverteilung)
- W.20.09 | beidseitige Konfidenzintervalle (über Tabelle der Binomialverteilung)
- W.20.10 | einseitige Konfidenzintervalle (über Tabelle der Binomialverteilung)
- W.20.11 | beidseitige Hypothesentests (über Tabelle der Binomialverteilung)
- W.20.12 | einseitige Hypothesentests (über Tabelle der Binomialverteilung)
- W.20.13 | Formel für 95%-Konfidenzintervall
- W.20.14 | Formel für Irrtumswahrscheinlichkeit von 5%



