Oberstufe

W.19 | Poisson-Verteilung

Die „Poisson-Verteilung“ wendet man vor allem bei Ereignissen an, die eine recht kleine Wahrscheinlichkeit haben. Man nennt die Poisson-Verteilung daher auch „Verteilung der seltenen Ereignisse“. Mit ihrer Hilfe berechnet man, mit welcher W.S. ein Ereignis in EINEM bestimmten Intervall „k“ mal eintrifft. Es gibt nur zwei Größen, die in die Formel einfließen: „k“ (das ist die Häufigkeit mit der das Ereignis eintreffen soll) und „lambda“ (das ist die Häufigkeit mit der man das Ereignis in diesem Intervall durchschnittlich erwartet).

 

Die Poissonverteilung verwendet man bei sehr kleinen Wahrscheinlichkeiten, weswegen die Poissonverteilung auch die „Verteilung der seltenen Ereignisse“ heißt.
Witziger Weise fließt aber die W.S. gar nicht in die Poisson-Verteilung ein, sondern nur der Erwartungswert.

Man verwendet die Poisson-Verteilung in folgender Situation:
Es gibt ein zufälliges Ereignis, das immer wieder eintrifft und man weiß wie oft dieses Ereignis im Durchschnitt eintrifft. Das reicht schon um auszurechnen mit welcher W.S. es einmal, zweimal, dreimal, … x-mal eintreffen wird.

 

Man berechnet mit der Poisson-Verteilung die W.S., dass innerhalb einer bestimmten Zeiteinheit ein bestimmtes Ereignis genau „k“ mal eintrifft.

 

 

k ist die Anzahl der Zeiteinheiten
λ ist der Erwartungswert

 

Bevor wir noch ewig drum herum reden, erklären wir die Poisson-Verteilung anhand von Rechenbeispielen.

 

Beispiel a.

Ein kleines Hotel in Paris hat einen Mini-Aufzug, in welchen nur vier Leute reinpassen. Der Aufzug fährt immer hoch und runter, wie es sich eben für funktionierende Aufzüge gehört.
Jedes Mal wenn der Aufzug im Erdgeschoss an der Rezeption ankommt, warten bereits ein paar Gäste. Im Schnitt sind es zwei Personen.
a) Mit welcher W.S. warten genau zwei Personen?
b) Mit welcher W.S. wartet niemand unten?
c) Mit welcher W.S. warten mehr als vier Leute unten, so dass nicht alle reinpassen?

Lösung:

Man müsste natürlich nicht zwingend die Poisson-Verteilung anwenden, aber man kann sie anwenden.
Für die Poisson-Verteilung braucht man eigentlich nur den Erwartungswert.
Dieser ist in unserer Aufgabe E(x)=2. In der Poission-Verteilung heißt er λ=2.

a) Nur weil durchschnittlich zwei Personen auf den Aufzug warten, heißt es natürlich nicht, dass das immer zwei Leute warten. Wir brauchen hier die W.S. dafür.

Der Erwartungswert beträgt: λ=2. Die Anzahl der Leute, die warten sollen, ist ebenfalls 2 ⇒ k=2.

 

b) Nun soll niemand unten warten ⇒ k=0. E(x) liegt unverändert bei λ=2.

 

c) Es sollen mehr als vier Leute warten. Das sind leider prutahl-viele Fälle. (nämlich 5 Leute, 6, 7, 8, … ∞). Um diese Fälle alle zu berechnen braucht man sehr lange. Wir verwenden eine wahnsinnig schlauen Trick und berechnen das Gegenereignis.
Das Gegenereignis von „mehr als vier“ ist „vier oder weniger“, beinhaltet also die Fälle: x=0, x=1, x=2, x=3 und x=4.

 

 

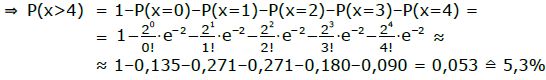
Beispiel b.

In einem kleinen Provinzstädtchen hagelt es alle fünf Jahre schlimme Schäden.
a) Mit welcher W.S. hagelt es in einem bestimmten Jahr zwei Mal?
b) Mit welcher W.S. hagelt es in innerhalb von zwei Jahren genau ein Mal?
c) Mit welcher W.S. fällt innerhalb der nächsten vier Jahre kein Hagel?

Lösung:

Wir wenden natürlich die Poisson-Verteilung an, weil das schön ist.
Dafür brauchen wir den Erwartungswert.
Da es im Schnitt einmal alle fünf Jahre hagelt, ist der Erwartungswert von einem Hagelschaden bei einem Fünftel pro Jahr.
Wenn wir für Teilaufgabe b) einen Zeitraum von zwei Jahren betrachten, ist der Erwartungswert für die Anzahl der Hagelschäden zwei Fünftel. Bei vier Jahren ist der Erwartungswert vier Fünftel, usw. [Alles wegen der Formel E(x)=n·p].

a) Der betrachtete Zeitraum liegt bei einem Jahr. Da es im Schnitt einmal alle fünf Jahre hagelt, liegt die durchschnittliche Hagelhäufigkeit pro Jahr bei 1/5=0,2.
λ ist der Erwartungswert für die jeweils betrachtete Zeiteinheit, also λ=0,2.
k ist die gewünschte Häufigkeit des Ereignisses pro Zeiteinheit. Hier gilt k=2, da es in dem einen Jahr zwei Mal hageln soll.

b) Der betrachtete Zeitraum beträgt zwei Jahre. Für ein Jahr liegt der Erwartungswert bei 0,2 Hagelschäden [siehe Teilaufgabe a)]. Für zwei Jahre liegt der Erwartungswert bei E(x)=n·p=2·0,2=0,4 ⇒ λ=0,4.
k ist die gewünschte Häufigkeit des Ereignisses pro Zeiteinheit. Hier gilt k=1, da es in diesen zwei Jahren einmal Mal hageln soll.

 

Beispiel c.

Im Durchschnitt fallen auf jeden Quadratkilometer der Erdoberfläche alle 1.000 Jahre vier Meteoriten [die Zahlen stimmen in etwa].
Bero kauft in Georgien ein Grundstück von der Größe eines Quadratkilometers.

a) Mit welcher WS. fällt innerhalb der nächsten 2000 Jahre genau ein Meteorit?
b) Mit welcher WS. fällt innerhalb der nächsten 2000 Jahre mindestens ein Meteorit?
c) Mit welcher WS. würde innerhalb der nächsten 60 Jahre mindestens ein Meteorit auf ein zehn mal größeres Grundstück fallen?
d) Mit welcher WS. fällt in einer bestimmten Minute irgendwo auf der Erde [ca. 500 Mio. km²] mindestens ein Meteorit?

Lösung:

Poisson-Verteilung ist toll.
Wir haben hier zwei „Grundeinheiten“: einerseits die Zeit, andererseits die Grundfläche. Beides ist kein Problem, wir müssen es nur im Hinterkopf behalten.
Als Basis gehen wir von einem Quadratkilometer aus und von 1000 Jahren. Hier werden vier Meteoriten erwartet, es gilt also: für 1km² und 1000 Jahre: λ=4

a) Für 1km² und 1000 Jahre werden vier Meteorit erwartet. Für 1 km² und 2000 Jahre werden 2 mal mehr Meteoriten erwartet, also λ=8. Es soll genau ein Meteorit fallen ⇒ k=1.

b) Für λ gilt natürlich unverändert λ=8. Allerdings soll nicht genau ein Meteorit fallen, sondern mindestens einer. Das sind viele Fälle [k=1, k=2, k=3, … k=∞], daher verwenden wir das Gegenereignis, also den Fall k=0.

 

c) Für 1km² und 1000 Jahre werden vier Meteoriten erwartet, hierfür gilt also λ=4.
Betrachtet man die Zeitspanne von 60 Jahren, so ist das ⁶⁰/₁₀₀₀=0,06 mal mehr, es gilt λ=4·0,06=0,24. Die Fläche wird nun 10 mal größer, das sollte also bedeuten, dass auch 10 mal mehr Meteoriten runter fallen. ⇒ λ=0,24·10=2,4.

Mindestens ein Meteorit ist das Gegenereignis von kein Meteorit, welches wir zuerst berechnen.

 

 

d) Für 1km² und 1000 Jahre werden vier Meteorit erwartet.
Für die Erdoberfläche mit 500 Mio werden [auf 1000 Jahre] damit 500Mio·4 = 2000 Mio Meteoriten erwartet.
Während eines Jahres werden [immer noch pro Erdoberfläche] 2000 Mio / 1000 = 2Mio Meteoriten erwartet.
Während eines Tages werden 2Mio / 365 ≈ 5479,4 Meteoriten erwartet.
Während einer Stunde sind´s 5479,4 / 24 ≈ 228,3 Stück und während einer Minute sind´s 228,3 / 60 ≈ 3,8 Stück

Nochmal: In jeder Minute rechnet man mit durchschnittlich 3,8 Meteoriten, die irgendwo auf der Erdoberfläche niedergehen ⇒ λ=3,8.