Oberstufe

A.13.03 | Kettenregel

Die Kettenregel wendet man an, wenn man verkettete Funktionen hat bzw. wenn man irgendwelche sauschwierigen Klammern ableiten muss (z.B. Klammern mit Hochzahlen oder Klammern mit sin/cos, …). Die Hauptaussage der Kettenregel ist die, dass die innere Ableitung mit „Mal“ verbunden hinten angehängt werden muss.

 

 Bevor du dieses Video anschaust, solltest du dieses Thema beherrschen:

>>> [A.13.01] Polynome ableiten

---

 Sobald du dieses Video verstehst, kannst du auch folgendes Thema angehen:

>>> [A.13.06] Vermischte Aufgaben

>>> [A.13.07] vermischte Funktionstypen

---

 

Lerntipp:
Versuche die Beispiele zuerst selbstständig zu lösen, bevor du das Lösungsvideo anschaust.

 

Rechenbeispiel 1

Bestimmen Sie die Ableitung der Funktion über die Kettenregel f(x)=2·(3x+1)⁴

   Lösung dieser Aufgabe

 

Rechenbeispiel 2

Bestimmen Sie die Ableitung der Funktion über die Kettenregel g(x)=4·(4–2x³)²

   Lösung dieser Aufgabe

 

Rechenbeispiel 3

Bestimmen Sie die Ableitung der Funktion über die Kettenregel

   Lösung dieser Aufgabe

 

Rechenbeispiel 4

Bestimmen Sie die Ableitung der Funktion über die Kettenregel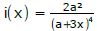

   Lösung dieser Aufgabe

 

Rechenbeispiel 5

Bestimmen Sie die Ableitung der Funktion über die Kettenregel

   Lösung dieser Aufgabe

 

Rechenbeispiel 6

Bestimmen Sie die Ableitung der Funktion über die Kettenregel

   Lösung dieser Aufgabe