Oberstufe
A.13 | Ableitungen
Was ist eine Ableitung überhaupt ?
Die Ableitung einer Funktion f(x) gibt die Steigung bzw. die Tangentensteigung an. Die Funktion f(x) muss man ableiten und in die Ableitung f'(x) den x-Wert des Punktes einsetzen um den es geht. Das Ergebnis ist die Steigung der Funktion an der Stelle (bzw. die Tangentensteigung).
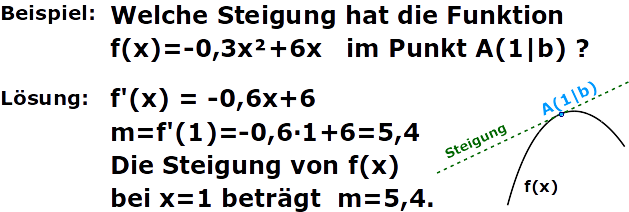
Bei anwendungsbezogenen Aufgaben ist die Ableitung die Zunahme bzw. die Abnahme (je nach Vorzeichen).
Warum gibt es verschiedene Ableitungsregeln ?
Fast jeder Funktionstyp hat eine andere Ableitungsregel, d.h. man muss die verschiedenen Ableitungsregeln von Polynomen, Exponentialfunktionen, sin- und cos-Funktionen kennen.
Bei schwierigen Funktionen muss man (abgesehen von den „normalen“ Ableitungsregeln) noch drei spezielle Regeln angewendet werden: die Kettenregel, die Produktregel und die Quotientenregel. Wir werden diese drei Ableitungsregeln in Kapitel A.13.03 bis A.13.05 gesondert behandeln.
„Ableiten“ nennt man auch „Differenzieren“.

 Es gibt themenverwandte Videos, die dir auch helfen könnten:
Es gibt themenverwandte Videos, die dir auch helfen könnten:
>>> [A.11.03] f''(x) = Linkskrümmung / Rechtskrümmung
>>> [A.41.03] Ableitungen bei e-Funktionen (Basiswissen), [A.41.04] Ableitungen bei e-Funktionen (Herausforderung)
>>> [A.42.04] Ableitungen bei sin/cos-Funktionen (Basiswissen), [A.42.05] Ableitungen bei sin/cos-Funktionen (Herausforderung)
>>> [A.43.02] Ableitungen bei gebrochen-rationalen Funktionen (Basiswissen), [A.43.03] Ableitungen bei gebrochen-rationalen Funktionen (Herausforderung)
>>> [A.44.02] Ableitungen bei Logarithmus-Funktionen (Basiswissen), [A.44.03] Ableitungen bei Logarithmus-Funktionen (Herausforderung)
>>> [A.45.01] Ableitungen bei Wurzel-Funktionen (Basiswissen), [A.45.02] Ableitungen bei Wurzelfunktionen (Herausforderung)
[A.13.01] Polynom ableiten
Ein Polynom leitet man so ab: die Hochzahl vom x-Term kommt mit „mal“-verbunden vor den Term, die neue Hochzahl wird um 1 kleiner.
Aus x4 wird also 4·x³, aus 4x³ wird 4·3·x²=12x²
Bei Termen der Form „Zahl·x“ fällt das „x“ weg. Aus „5x“ wird also „5“.
Zahlen, die kein „x“ haben, fallen weg.
f(x) = a·xn
f'(x) = a·n·xn-1

Beispiel a.
Leiten wir die Funktion f(x)=x4+4x3–7x2+5x–2 ab.
Lösung:
f(x) = x4 + 4x3 – 7x2 + 5x – 2 ableiten ...
f'(x) = 4·x³+4·3x² –7·2x + 5 vereinfachen ...
= 4x³ + 12x² – 14x + 5
[Will man f´(x) ein weiteres Mal ableiten, dann ist das die zweite Ableitung.]
f'(x) = 4x³ + 12x² – 14x + 5
f''(x) = 4·3x² + 12·2x – 14
= 12x² + 24x – 14
Beispiel b.
f(x) = x5 + 4x4 – 2x3 – 5x2 + 3x + 3,2
f'(x) = 5x4+4·4x3 –2·3x2 –5·2x + 3
= 5x4 +16x3 – 6x2 – 10x +3
f''(x) = 20x³+48x²–12x–10
[A.13.02] einfache Wurzel und Bruch ableiten
Wurzeln und Brüche sollte man zuerst umschreiben:
Bei Brüchen der Form bringt man den Nenner von unten hoch, in den Zähler, in dem man das Vorzeichen der Hochzahl ändert.
Wurzeln schreibt man um, in dem man aus der Hochzahl von „x“ einen Bruch macht.


[A.13.03] Verkettung ableiten (Kettenregel)
Die Kettenregel wendet man an, wenn man verschachtelte Funktionen hat. [„Verschachtelte Funktionen“ bedeutet nomalerweise: Funktionen mit Klammern drin.]
Die Kettenregel sagt, dass man immer die innere Ableitung hinter die Funktion dran hängen muss [sofern eine innere Ableitung existiert] !
Die Kettenregel: f(x)= u(v(x)) ⇒ f'(x)=u'(v(x))·v'(x)

Beispiel h.
Was ist die Ableitung von f(x) = (2x+5)13 ?
Lösung:
Um f(x) abzuleiten, denkt man zuerst nur an (...)13.
(...)13 abgeleitet ergibt 13·(...)12.
Erst anschließend betrachtet man das Innere der Klammer „(2x+5)“, leitet dieses zu „2“ ab und hängt diese „2“ hinten an die Ableitung dran.
f(x)=(2x+5)13 gibt abgeleitet: f'(x) = 13·(2x+5)12·2
Beispiel i.

Beispiel j.
Um Wurzeln abzuleiten, sollte man diese immer zuerst umschreiben.

[A.13.04] Produkte ableiten mit der Produktregel (Leibnizregel)
Die Produktregel (sie heißt auch „Leibnizregel“) verwendet man selbstverständlich dann, wenn man ein Produkt ableiten muss.
Zum Beispiel ist das zwingend notwendig bei: f(x) = x·sin(x) oder g(x) = (x–2)·e4–x
Bevor wir uns jedoch an Themen von [A.41] Exponentialfunktionen und [A.42] Trigonometrische Funktionen wagen (Sinus- und e-Funktionen), üben wir Leichteres.
Die Produktregel: f(x)= u·v ⇒ f'(x)=u'·v+u·v'


[A.13.05] Brüche ableiten mit der Quotientenregel
Bruch-Funktionen heißen eigentlich gebrochen-rationale Funktionen und sind in [A.43] Gebrochen-Rationale Funktionen ausführlicher beschrieben.
Wir gehen daher hier nur kurz auf die Quotientenregel ein. Nennen wir also den Zähler [=das Obere] „u“, und den Nenner [=das Untere] „v“.
Einen Bruch ableiten kann man so:
.jpg)

[A.13.06] Vermischte Aufgaben - Kombination der Ableitungsregeln
Beispiel r.
Leiten wir f(x) = 3x2·(2x+1)4 ab.
[Wenn man f(x) betrachtet, sieht man zwei Terme, die mit „mal“ verbunden sind: nämlich „3x²“ und „(2x+1)4“.
Daher braucht man die Produktregel. Ein Teil des Produkts ist v=(2x+1)4. Um dieses abzuleiten, braucht man die Kettenregel.]
f'(x) = 6x·(2x+1)4 + 3x²·8(2x+1)3
[hier kann man noch vereinfachen, wenn man (2x+1)3 ausklammert]
= (2x+1)3 · [ 6x·(2x+1) + 3x²·8 ] =
= (2x+1)3 · [ 12x²+6x + 24x² ] =
= (2x+1)3 · ( 36x²+6x )
Beispiel s.
Wir wollen die Ableitung der Funktion:



